If you jump out of an airplane, how fast would you fall? What's the greatest speed you would reach? Let's practice figuring it out without jumping out of a plane.
This experiment will help you get the concept of velocity by allowing you to measure the rate of fall of several objects. It's also a great experiment to record in your
science journal.
First, you'll need to find your materials:
[am4show have='p8;p9;p12;p39;p72;p92;' guest_error='Guest error message' user_error='User error message' ]
- stop watch
- feathers (or small pieces of paper, plastic bag or anything light and fluffy)
- a tape measure
- If you're crunching numbers, you'll also need a calculator.
Now here's how to do the experiment:
1. Get 5 or so different light and fluffy objects. Feathers of different size, small strips of paper, parts of a plastic bag, cotton balls, whatever is handy.
2. Make a prediction by writing down the objects you chose in order of how fast you think they will fall. The fastest on top, the slowest on the bottom. Leave space to the right of your prediction so that you can write in your conclusions and then compare the two.
3. Make a table with two columns. Use one column to fill in the name of the items. Use the second column to write down the time it took each object to fall.
4. Drop the different items and time them from the moment you let go to the moment they hit the ground. Be sure to drop each item from about the same height. The higher the better. Just be sure not to fall off anything! We don’t want to measure your velocity!! You might want to drop them two or three times to get an average time.
5. Now compare the items. Which one fell the least amount of time (dropped the fastest)? Which one fell the most amount of time (dropped the slowest)? Write your results next to your hypothesis. By the way, did you find anything that dropped slower than a feather? I have seen very few things that take longer to fall straight down than a feather.
Download Student Worksheet & Exercises
Did you see how many of your objects stopped accelerating very quickly? In other words, they reached their terminal velocity soon after you let them go and they fell all the way to the ground at that same constant velocity. This is why a parachute is a sky-diver’s best friend! A human has a decent amount of air resistance but he or she can reach a lethal dose of velocity (120 mph) if dropped from a great height. The parachute increases the air resistance so that the terminal velocity of that sky-diver is quite a bit safer!
Exercises
- What is velocity?
- How do acceleration and deceleration relate to velocity?
- How do we know when an object has reached terminal velocity?
Taking it Further for advanced students:
[/am4show]
[am4show have='p9;p39;' guest_error='Guest error message' user_error='User error message' ]
We can do a little math here and figure out the actual velocity of your objects. Here's how to do it:
Measure the height from which you dropped each object. Now take the height of the drop and divide that by the number of seconds it took for it to drop that distance. That’s the velocity of that object. For example, My “from-under-the-couch-six-month-old-dust-bunny” took 3 seconds to fall 6 feet. I take 6 feet and divide it by 3 seconds to get 2 feet/second.
The velocity of my dust bunny is 2 feet/second downward.
Remember, that velocity has a directional component as well as a number. Add a little more math, and I can predict how long my dust bunny will take to fall 15 feet. Take the distance (15 feet) and divide it by the velocity (2 feet/second) and I get 7.5 seconds. It will take my dust bunny 7.5 seconds to fall 15 feet. Hmmm, maybe we should call it a dust snail.
Have you noticed something here? In
this experiment, we used a different formula to find out how far something would fall over a given time.
What’s going on? In
Unit 1, we ignored their terminal velocity. Those things were in free fall and accelerating (gaining velocity) all the way to the ground. They were never going the same velocity for the entire trip. So, we needed to use the gravitational constant 32 ft/s² in the equation d=1/2 gt² to determine how far something fell in a given amount of time.
For this unit, we are dealing with things that are at an almost constant velocity, (since they reach their terminal velocity quickly) so we can use the much simpler equation d=vt (d is distance, v is velocity and t is time). In the problems we’ve done in this lesson plan, we have modified that formula to find how long the fall took so we’ve used t=d/v.
If you’d like to solve for v you would use v=d/t. Isn’t algebra fun?
Advanced students: Download your
terminal velocity lab here.
[/am4show]
You have just taken in a nice bunch of information about the wild world of gravity. This next section is for advanced students, who want to go even deeper. There's a lot of great stuff here but there's a lot of math as well. If you're not a math person, feel free to pass this up. You'll still have a nice understanding of the concept. However, I'd recommend giving it a try. There are some fun things to do and if you're not careful, you might just end up enjoying it!
Here's what you need:
[am4show have='p9;p38;p92;' guest_error='Guest error message' user_error='User error message' ]
- ball
- pencil, paper
- stopwatch
- yardstick or tape measure
Download Student Worksheet & Exercises
Okay, let’s see where we can go here. Gravity accelerates all things equally...what does that mean? All things accelerate at 32 feet per second squared due to gravity. In metric, it accelerates 9.8 meters per second squared.
What that means is, every second something falls, its speed increases by 32 feet/second or 9.8 meters/second. Believe it or not, that’s about 22 miles per hour!! Gravity will accelerate something from 0 to 60 mph in about 3 seconds. Faster then all but the fastest sports cars!
So what is acceleration anyway? Well speed is the amount of distance something travels in a certain amount of time. Five miles per hour, for example, tells you that something can travel five miles in an hour. Acceleration is how much the speed changes over time. So acceleration would be miles per hour per hour or feet per second per second.
Acceleration is a rate of change of speed or, in other words, how fast is the speed is changing. Feet per second per second is the same as ft/s/s which is the same as ft/s². (I told you we were going deeper!) Let’s say you’re riding your bicycle at a positive acceleration (your getting faster) of 5 ft/s².
That means in 1 second you’re moving at a speed of 5 ft/s.
After 2 seconds you’re moving at a speed of 10 ft/s.
After 3 seconds you’re now clipping along at 15 ft/s (about 10 mph).
So you can see that as long as you accelerate, you will be getting faster and faster. The formula for this is v=at where v is velocity, a is acceleration and t is time. (We will be doing more with acceleration in a future lesson.)
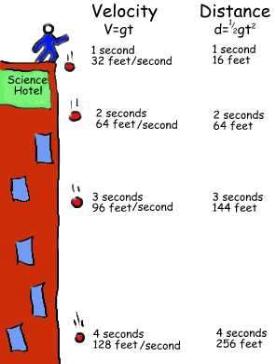
If we want to find out how fast something is going after it has been dropped, we use the formula v=gt. The letter “v” stands for velocity (which basically means speed.) “g” stands for the gravitational constant and “t” stands for time.
If we want to find out how fast a golf ball is dropping after it falls for 3 seconds we multiply 3 seconds by 32 feet/second squared and that equals 96 feet/second. So, if I dropped a golf ball off a building, it would be going 96 feet per second after 3 seconds of dropping.
The formula looks like this when we fill in the numbers:
v=3s x 32 ft/s²
If we do more math, we’ll see that after one second something will be item7going 32 ft/s, after 2 seconds it will be going 64 ft/s, after 3 seconds 96 ft/s after 4 seconds 128 ft/s. Get it? Anything dropped will be going that speed after that many seconds because gravity accelerates all things equally (air resistance will effect these numbers so you won’t get exactly the numbers in practice that you will mathematically).
All right, lets go even deeper. We now know how to calculate how fast something will be going if it is dropped, but what happens if we throw it up? Well, which way does gravity go? Down right? Gravity accelerates all things equally so, gravity will slow things down as they travel up by 32 ft/s². If a ball is thrown up at 64 ft/s how long will it travel upwards? Well, since it is negatively accelerating (in physics there’s no such thing as deceleration) after the first second the ball will be traveling at 32 ft/s and after 2 seconds the ball will come to a stop, turn around in midair, and begin to accelerate downwards at 32 ft/s². Using this, you can tell how fast you can throw by using nothing more then a timer. Let's try it.
For this experiment, you will need:
- A ball (a tennis ball or baseball would be perfect)
- A stopwatch
- Pencil and paper
- A friend
- A calculator
1. Go outside and pick one person to be the thrower and another to be the timer.
2. Have the timer say "Ready, Set, Go!" and at go he or she should start the stopwatch.
3. When the timer says go, the thrower should toss the ball as high as he or she can.
4. The timer should stop the stopwatch when the ball hits the ground.
5. Write down the time that the ball was in the air.
6. Let each person take a couple of turns as timer and thrower.
7. Now, come back inside and do a bit of math.
Ok, let's see how you did. Let’s say you threw the ball into the air and it took 3 seconds to hit the ground. The first thing you have to do is divide 3 in half. Why? Because your ball traveled 1.5 seconds up and 1.5 seconds down! (By the way, this isn’t completely accurate because of two things. One, air resistance and two, the ball falls a little father then it rises because of the height of the thrower.) Now, take your formula and figure out the speed of the throw.
v=gt,
so v=32 ft/s² x 1.5 sec or
v = 48 ft/s.
So, if that’s how fast it left your hand...how fast was it going when it hit the ground? Yup, 48 ft/s. It has to be going the same speed because it had just as much time to speed up as it had to slow down, 1.5 seconds. Try that with your time and see how fast your throw was.
Ok, hold your breath, just a little deeper now. Let’s talk about distance. If something starts from rest you can tell how far it drops by how long it has dropped. This formula is d=1/2gt² or distance equals one half the gravitational constant multiplied by time squared. Let’s try it. If I drop a ball and it drops 3 seconds how far has it dropped?
d=1/2 32ft/s² x (3s)² or
d = 16 ft/s x 9s² or
d=144 ft So it has dropped 144 ft.
Now try this with your time. What's the first thing you have to do? Divide your time in half again, right. It took your ball half the time to go up and half the time to come down. Now plug your numbers into 1/2gt² and find out how high you threw your ball! Is Major League Baseball in your future?!
Advanced students: Download your
Fast Ball Lab here.
Exercises
- Is gravity a speed, velocity, or acceleration?
- Does gravity pull equally on all things?
- Does gravity accelerate all objects equally?
- How is acceleration different from speed and velocity?
[/am4show]
If I toss a ball horizontally at the exact same instant that I drop another one from my other hand, which one reaches the ground first? For this experiment, you need: [am4show have='p8;p9;p11;p38;p72;p92;' guest_error='Guest error message' user_error='User error message' ]
- 2 rulers or paint sticks. Any thing wide and flat
- 2 coins or poker chips
- A sharp eye and ear
- A partner is good for this one too
Download Student Worksheet & Exercises
1. Place one of the rulers flat so that it is diagonal across the edge of a table with half the ruler on the table and half sticking off.
2. Place one coin on the table, just in front of the ruler and just behind the edge of the table. Place the other coin on the ruler on the side where it’s off the table.
3. Put your finger right in the middle of the ruler on the table so that you are holding it in such a way that it can spin a bit under your finger. Now with the other ruler you are going to smack the end of the first ruler so that the first ruler pushes the coin off the desk and the coin that’s resting on the ruler falls to the ground.
4. Now, before you smack the ruler, make a prediction. Will the coin that falls straight down or the coin that is flying forward hit the ground first?
5. Try it. Do the test and look and listen carefully to what happens. It’s almost better to use your ears here than your eyes. Do it a couple of times.
Are you surprised by what you see and/or hear? Most people are. It’s not what you would expect.
The coins hit the ground at the SAME time. Is that odd or what?

Did you read the first sentence at the top of this lab? What do you think will happen?
The balls will hit the ground at the exact SAME time.
Gravity doesn’t care if something is moving horizontally or not. Everything falls toward the center of the Earth at the same rate.
Let me give you a better example: A bullet fired parallel to the ground from a gun and a bullet dropped from the same height at the same time will both hit the ground at the same time. Even though the one fired lands a mile away! It seems incredible, but it’s true.
Gravity doesn’t care what size something is or whether or not it is moving, Gravity treats all things equally and accelerates them the same.
Notice, that I say gravity accelerates all things equally, not gravity
pulls on all things equally. Gravity does pull harder on some things than on other things. This is why I weigh more than a dog. I am made of more stuff (I have more atoms) than the average dog, so gravity pulls on me more.
Weight is nothing more than a measure of how much gravity is pulling on you. This is why you can be “weightless” on a scale in space. You are still made of stuff, but there’s a balance of the gravity that is pulling on you and the outward force due to the acceleration since you’re moving in a circle (which you do in order to remain in orbit), so it
feels like you have no weight.
The larger a body is, the more gravitational pull or the larger a gravitational field it will have.
The Moon has a fairly small gravitational field (if you weighed 100 pounds on Earth, you’d only be 17 pounds on the Moon), the Earth’s field is fairly large and the Sun has a HUGE gravitational field (if you weighed 100 pounds on Earth, you’d weigh 2,500 pounds on the sun!).
As a matter of fact, both the dog and I both have gravitational fields! Since we are both bodies of mass we have a gravitational field which will pull things towards us. All bodies have a gravitational field. However, my mass is sooooo small that the gravitational field I have is miniscule. Something has to be very massive before it has a gravitational field that noticeably attracts another body.
So what’s the measurement for how much stuff you’re made of? Mass. Mass is basically a weightless measure of how much matter makes you, you. A hamster is made of a fairly small amount of stuff so she has a small mass. I am made of more stuff, so my mass is greater than the hamster’s. Your house is made of even more stuff so its mass is greater still.
So, here’s a question. If you are “weightless” in space, do you still have mass? Yes, the amount of stuff you’re made of is the same on Earth as it is in your space ship. Mass does not change but since weight is a measure for how much gravity is pulling on you, weight will change.
Did you notice that I put weightless in quotation marks? Wonder why?
Weightlessness is a myth! Believe it or not, one is never weightless. A person can be pretty close to weightless in very deep space but the astronauts in a space ship actually do have a bit of weight.
Think about it for a second. If a space ship is orbiting the Earth what is it doing? It’s constantly falling! If it wasn’t moving forward at 10’s of thousands of miles an hour it would hit the Earth. It’s moving fast enough to fall around the curvature of the Earth as it falls but, indeed, it’s falling as the Earth’s gravity is pulling it to us.
Otherwise the ship would float out to space. So what is the astronaut doing? She’s falling too! The astronaut and the space ship are both falling to the Earth at the same rate of speed and so the astronaut feels weightless in space. If you were in an elevator and the cable snapped, you and the elevator would fall to the Earth at the same rate of speed. You’d feel weightless! (Don’t try this at home!)
Exercises
- True or false? Gravity pulls on all things equally.
- True or false? Gravity accelerates all things equally.
- In your own words, why do the coins hit the ground at the same time? Is this what you’d expect to happen on Mars?
The rest of this experiment is for advanced students...[/am4show]
[am4show have='p9;p38;' guest_error='Guest error message' user_error='User error message' ]
For advanced students:
Either now, or at some point in the future you may ask yourself this question, "How can gravity pull harder (put more force on some things, like bowling balls) and yet accelerate all things equally?" When we get into Newton's laws in a few lessons you'll realize that doesn't make any sense at all. More force equals more acceleration is basically Newton's Second law.
Well, I don't want to take too much time here since this is a little deeper then we need to go but I do feel some explanation is in order to avoid future confusion. The explanation for this is inertia. When we get to Newton's First law we will discuss inertia. Inertia is basically how much force is needed to get something to move or stop moving.
Now, lets get back to gravity and acceleration. Let's take a look at a bowling ball and a golf ball. Gravity puts more force on the bowling ball than on the golf ball. Soooo the bowling ball should accelerate faster since there's more force on it. However, the bowling ball is heavier soooo it is harder to get it moving. Vice versa, the golf ball has less force pulling on it but it's easier to get moving. Do you see it? The force and inertia thing equal out so that all things accelerate due to gravity at the same rate of speed!
Gravity had to be one of the first scientific discoveries. Whoever the first guy was to drop a rock on his foot, probably realized that things fall down! However, even though we have known about gravity for many many years, it still remains one of the most elusive mysteries of science. At this point, nobody knows what makes things move towards a body of mass.
Why did the rock drop towards the Earth and on that guy's foot? We still don't know. We know that it does, but we don't know what causes a gravitational attraction between objects. Gravity is also a very weak force. Compared to magnetic forces and electrostatic forces, the gravitational force is extremely weak. How come? No one knows. A large amount of amazing brain power is being used to discover these mysteries of gravity. Maybe it will be you who figures this out!
Advanced students: Download your
Forever Falling Lab here.
[/am4show]
Click here to go to next lesson on Force and Mass.


 So you can see that as long as you accelerate, you will be getting faster and faster. The formula for this is v=at where v is velocity, a is acceleration and t is time. (We will be doing more with acceleration in a future lesson.)
So you can see that as long as you accelerate, you will be getting faster and faster. The formula for this is v=at where v is velocity, a is acceleration and t is time. (We will be doing more with acceleration in a future lesson.) Did you read the first sentence at the top of this lab? What do you think will happen?
Did you read the first sentence at the top of this lab? What do you think will happen?
 This experiment is one of my favorites in this acceleration series, because it clearly shows you what acceleration looks like.
The materials you need is are:
This experiment is one of my favorites in this acceleration series, because it clearly shows you what acceleration looks like.
The materials you need is are: